组合数学常用公式

二项式定理

二项式系数相关性质：

• 对称性：$C_n^m = C_n^{n-m}$

• 增减性与最大值：二项式系数前半部分逐渐增大，后半部分逐渐减小，中间取最大值。

  $$\text{最大值} max=\begin{cases} C_n^{\frac{n}{2}} \\ C_n^{\frac{n-1}{2}}=C_n^{\frac{n+1}{2}}\end{cases}$$

• 二项式系数之和

  $$C_n^0+C_n^1+C_n^2+C_n^3+...+C_n^{n-1}+C_n^n=2^n$$

• 二项式奇数项系数之和等于偶数项系数之和，即

  $$C_n^1+C_n^3+C_n^5+...=C_n^0+C_n^2+C_n^4+C_n^6+...=2^{n-1}$$

杨辉三角

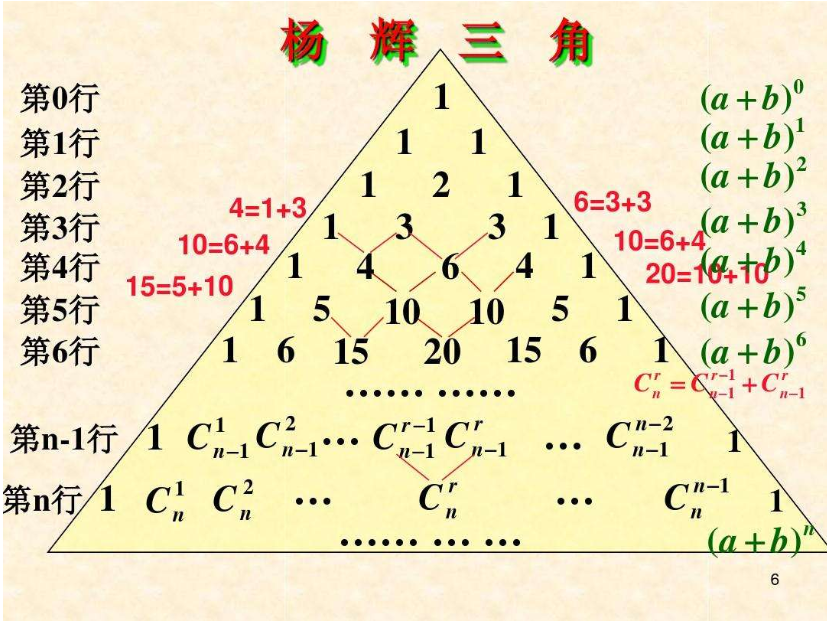
组合数公式

$C_n^m$计算

• 方式一：公式计算
  计算都是在逆元或者阶乘基础上计算的

$$C_n^m = \frac{n!}{m!*(n-m)!}$$

ll C(ll n, ll m)
{
	if(n < m) return 0;
	return fact[n] * invfac[m] % mod * invfac[n - m] % mod;
}

• 方式二：递推方式
  需要建表，所以如果计算范围比较大时需要的空间也大
  递推公式 ：

$$C_n^m = C_{n-1}^{m} + C_{n-1}^{m-1}$$

for(int i = 1; i <= n; i++)
	for(int j = 0; j <= i; j++)
	{
		if(i == j || j == 0) c[i][j] = 1;
		else c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
	}

排列组合方法

1. 隔板法

引入： 10 个相同小球放进 3 个不同盒子，每个盒子至少放进一个， 求种类数。

在10 个小球中间插入隔板， 共有 $10-1=9$ 个位置， 需要插入 $3-1=2$ 个隔板将其分成 3 部分。 共 $C_9^2 = 36$ 种。

• 一般隔板法：

将 $n$ 个相同的元素分成 $k$ 部分，每部分至少分得一个元素， 即在 $n-1$ 个空隙中插入 $k-1$ 个隔板，情况数为

$$C_{n-1}^{k-1}$$

等价于 $x_1+ x_2+x_3+...+x_k=n, x_i \geq 1$ 的可行解个数。

• 添元素隔板法：

将 $n$ 个相同的元素分成 $k$ 部分，每部分可以为空， 等价于我们先让元素个数添加上 $k$ 个，然后在 $n+k$ 个元素中分成 $k$ 部分， 最后再在 $k$ 部分的每一个部分都拿走一个元素，共拿走 $k$ 个元素。 即在 $n+k-1$ 个空隙中插入 $k-1$ 个隔板，情况数为

$$C_{n+k-1}^{k-1}$$

等价于 $x_1+ x_2+x_3+...+x_k=n, x_i \geq 0$ 的可行解个数。

此时该式可以转化为一般隔板法， 我们让 $x_i \geq 1$ 即可，操作是将每一个 $x_i$ 元素加上 $1$ ，相当于等式两边同时加了 $k$ ，即 $x_1+x_2+...+x_k=n+k,x_i \geq 1$ ，即可转化为一般隔板法。

• 隔板法应用

把10个相同的小球放到3个不同的箱子，第一个箱子至少1个，第二个箱子至少3个，第3个箱子可以为

空，有几种情况？

我们可以在第二个箱子先放入10个小球中的2个，小球剩8个放3个箱子，然后在第三个箱子放入8

个小球之外的1个小球（即补充了一个球），则问题转化为把9个相同小球放3不同箱子，每箱至

少1个，几种方法？

$C^2_8=28$