2022牛客多校1补题
题解有A C D G I J六题。
题解纯属自己玩,更多详细解释还请看官方题解。
G
题意
给定 ,将 视为不含前导零的字符串
求这些字符串中字典序最大的字符串
思路
只需要在 个9和 两个答案之中进行选择。
- 去除最后一位其余均为9,答案为
- 否则为 个9
复杂度 :
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
void solve()
{
string s;
cin >> s;
string t = string(s.size() - 1, '9');
if(s.substr(0, s.size() - 1) == t) cout << s << "\n";
else cout << t << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
t = 1;
// cin >> t;
while(t--)
solve();
return 0;
}A
题意
个区间 ,求 个区间并之后的区间的空隙长度和。
思路
贪心,将区间按左端点从小到大排序,从前往后扫一遍,不断维护维护区间右端点 。若当前区间的左端点小于 ,可以进行合并,并且更新区间右端点;若当前区间的左端点大于 ,计算答案。
注意第一个区间的判断以及 的初始值。
复杂度 :
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
void solve()
{
int n;
cin >> n;
vector<pii> a(n);
for(int i = 0; i < n; i++)
{
int c, r;
cin >> c >> r;
a[i] = {c - r, c + r};
}
sort(a.begin(), a.end());
ll ans = 0, rr = -1e18;
for(int i = 0; i < n; i++)
{
ll l = a[i].first, r = a[i].second;
if(l > rr && i)
ans += (l - rr);
rr = max(rr, r);
}
cout << ans << "\n";
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
t = 1;
// cin >> t;
while(t--)
solve();
return 0;
}D
题意
给定一个圆和严格位于圆内的一点
Mocha 会从点 向任意角度发射一个长度为 的电磁炮
电磁炮底边的中点为点P且两端位于圆内
询问单次发射能摧毁的最大圆弧长
思路
将电磁炮方向转化为竖直向上:无论当前的电磁炮旋转角度如何,我们可以固定电磁炮的方向,将点 绕原点旋转,从而使得电磁炮方向竖直向上(即 轴正方向)。
那么可以将题目转化成为电磁炮的方向总是竖直向上的,点 P 绕原点旋转一周的过程中可以摧毁的最长墙壁长度。
那么我们设点 P 到原点距离是 ,点 Q 绕原点旋转一周就可以转化成点Q在以 和 为端点的线段上移动。
下面用一张动图来说明:当点 Q 位于 轴上时,产生的弧长最长。
所以画图进行计算,我们计算弧度以此来算弧长。
当我们使用 计算时,因为正弦的 表示并不唯一,所以需要分情况讨论 和
当我们使用 计算时, 可以唯一表示 度,所以不需要分类讨论。
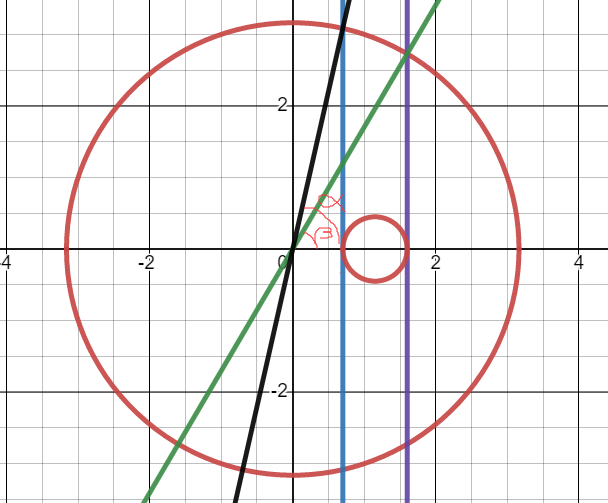
以 计算为例:
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
void solve()
{
int r, x, y, d;
cin >> r >> x >> y >> d;
double dis = sqrt(1ll * x * x + 1ll * y * y);
cout << fixed << setprecision(12);
double a = acos((dis + d) / r);
double b = acos((dis - d) / r);
cout << (b - a) * r << "\n";
// if(dis > d)
// {
// double a = asin((dis + d) / r);
// double b = asin((dis - d) / r);
// cout << r * (a - b) << "\n";
// }
// else
// {
// double a = asin((d + dis) / r);
// double b = asin((d - dis) / r);
// cout << r * (a + b) << "\n";
// }
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
t = 1;
cin >> t;
while(t--)
solve();
return 0;
}C
题意
一个二维平面,黑板为 的线段, 行 列座位在黑板前面,均为整数坐标。
个位置有人,求到黑板视线不被任何人挡住的座位数量。
次询问,修改一个人的坐标要求计算答案。
思路
每个人会挡住自己右边的人。每个人挡住的区域为一个折线右边的区域。
每次询问维护
: 纵坐标为 时最大不被遮挡的人的横坐标。
: 纵坐标为 时,被遮挡的座位的最小横坐标。
可以发现一个性质,当纵坐标从小到大时,如果新出现的点 与 构成的斜率更大,如果遮挡纵坐标更大的点时,也是该点遮挡后面的点。
时间复杂度 :
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
void solve()
{
int n, m, k, q;
cin >> n >> m >> k >> q;
vl x(k + 1), y(x), X(m + 1, n + 1), mn(m + 1, n);
for(int i = 1; i <= k; i++)
cin >> x[i] >> y[i];
while(q--)
{
int id;
cin >> id;
cin >> x[id] >> y[id];
for(int i = 1; i <= m; i++)
mn[i] = n, X[i] = n + 1;
for(int i = 1; i <= k; i++)
X[y[i]] = min(X[y[i]], x[i]);
int j = 0;
// 从下往上
for(int i = 1; i <= m; i++)
{
// (0, 1)(X[i], i) (0, 1)(X[j], j)
if(X[i] != n + 1 && (!j || (i - 1) * X[j] > (j - 1) * X[i]))
j = i;
if(j == 1)
mn[i] = min(mn[i], i == 1 ? X[i] - 1 : n);
else // y = kx+1 = (j - 1)/X[j] x + 1 = i
mn[i] = min(mn[i], j ? ((i - 1) * X[j] - 1) / (j - 1) : n);
}
j = 0;
for(int i = m; i >= 1; i--)
{
// (0,m)(X[i],i) (0,m)(X[j],j)
if(X[i] != n + 1 && (!j || (i - m) * X[j] < (j - m) * X[i]))
j = i;
if(j == m)
mn[i] = min(mn[i], i == m ? X[i] - 1 : n);
else // y = kx+m = (j-m)/X[j] x + m = i
mn[i] = min(mn[i], j ? ((m - i) * X[j] - 1) / (m - j) : n);
}
ll ans = 0;
for(int i = 1; i <= m; i++)
ans += mn[i];
cout << ans << "\n";
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
t = 1;
// cin >> t;
while(t--)
solve();
return 0;
}I
题意
初始手牌有13张麻将牌,相同牌至多出现2张
每轮可以从牌堆摸牌,若达成七对子则自摸胡牌
若不然则选择手牌中某张牌并丢弃之
给定初始手牌,求最优策略下达成七对子的期望轮数
多组数据,数据组数不超过 组
思路
期望DP
: 有 张单排,牌堆剩余 张的期望轮数
当 时,
初始手牌单牌数量为 ,答案为
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
ll f[150][15];
ll ksm(ll a, ll b)
{
ll res = 1;
while(b)
{
if(b & 1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res % mod;
}
void init()
{
for(int i = 1; i <= 123; i++)
{
ll inv = ksm(i, mod - 2);
for(int j = 1; j <= 13; j++)
{
f[i][j] = (1 +
f[i - 1][max(0, j - 2)] * (3 * j) % mod * inv % mod +
f[i - 1][j] * (i - 3 * j) % mod * inv % mod) % mod;
}
}
}
ll solve()
{
string s;
cin >> s;
int cnt = 0;
unordered_map<string, int> mp;
for(int i = 0; i < int(s.size()); i += 2)
{
if(mp[s.substr(i, 2)]) cnt--;
else cnt++;
mp[s.substr(i, 2)] ++;
}
return f[123][cnt];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
init();
int t;
t = 1;
cin >> t;
for(int i = 1; i <= t; i++)
cout << "Case #" << i << ": " << solve() << "\n";
return 0;
}J
题意
有一张 n 个点 m 条边的无重边无自环的有向图
初始时可以选择一个点染黑,其余点均为白点
若某个点所有入边的起点均为黑点,则该点可以被染黑
最大化图中黑点数量
思路
启发式合并。
当一个点的入度为 1 ,那么该点的前驱染黑的话,该点一定也被染黑。那么可以将该点和该点的前驱进行缩点合并看做一个集合。
因为每个点都可能会有对应的出边,而合并的两个点的出边可能会有重复,就要进行去重,因为缩点之后的出边只能有一条。去重就可以用到 set ,自带去重操作。
合并的时候也有技巧,通过出边数较小的点合并到出边数较大的点身上,也就是启发式合并(类似并查集中的合并),达到减小时间复杂度的目的。
递归合并即可,最后输出合并后最大的块。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
const int N = 2e5 + 5, M = N;
const int mod = 1e9 + 7;
int f[N], sz[N];
set<int> in[N], out[N];
int find(int x)
{
if(x == f[x])
return x;
return f[x] = find(f[x]);
}
void merge(int x, int y)
{
x = find(x), y = find(y);
if(x == y) return;
if(out[x].size() < out[y].size())
swap(x, y);
f[y] = x;
sz[x] += sz[y];
vi q;
for(auto v : out[y])
{
out[x].insert(v);
in[v].erase(y);
in[v].insert(x);
if(in[v].size() == 1)
q.push_back(v);
}
for(auto v : q)
merge(x, v);
}
int solve()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
in[i].clear(), out[i].clear();
f[i] = i;
sz[i] = 1;
}
for(int i = 1; i <= n; i++)
{
int k;
cin >> k;
for(int j = 1; j <= k; j++)
{
int u;
cin >> u;
in[i].insert(u);
out[u].insert(i);
}
}
for(int i = 1; i <= n; i++)
if(in[i].size() == 1)
merge(i, *in[i].begin());
int ans = 0;
for(int i = 1; i <= n; i++)
ans = max(ans, sz[i]);
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int t;
t = 1;
cin >> t;
for(int i = 1; i <= t; i++)
cout << "Case #" << i << ": " << solve() << "\n";
return 0;
}




